|
Дифференциальное уравнение n-го порядка в общем случае имеет вид:
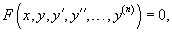 Порядок уравнения можно понизить, если оно не содержит некоторых аргументов или обладает определенной симметрией. Ниже мы рассмотрим подробнее некоторые случаи понижения порядка применительно к дифференциальным уравнениям произвольного n-го порядка. Преобразование уравнений 2-го порядка изложено здесь. Случай 1. Уравнение вида F(x, y (k), y (k+1),..., y (n)) = 0
Если дифференциальное уравнение не содержит исходной функции и ее k − 1 первых производных, то с помощью замены
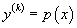 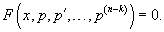 Если дифференциальное уравнение не содержит лишь исходную функцию y, т.е. имеет вид 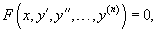 Случай 2. Уравнение вида F(y, y', y'',..., y (n)) = 0
Здесь левая часть не содержит независимой переменной x. Порядок уравнения можно понизить с помощью замены 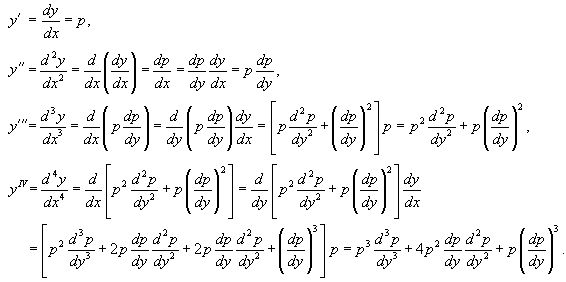 Случай 3. Однородное уравнение F(x, y, y', y'',..., y (n)) = 0
Уравнение 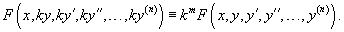 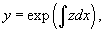 После определения 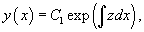 Случай 4. Функция F(x, y, y', y'',..., y (n)) является точной производной
В некоторых случаях левую часть 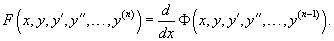 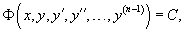 Рассмотрим примеры на различные случаи понижения порядка. |
|
Пример 1
|
|
Найти общее решение дифференциального уравнения
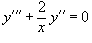 . .
Решение. 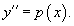 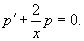 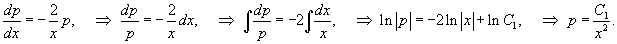 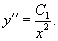 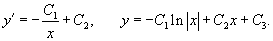 |
|
Пример 2
|
|
Найти общее решение уравнения
Решение. 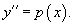 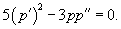 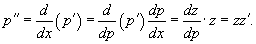 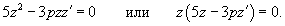 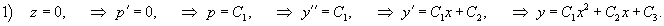 Найдем второе решение дифференциального уравнения. 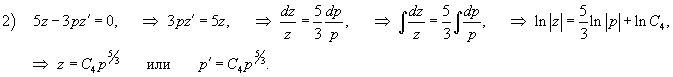 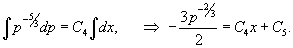 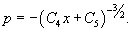 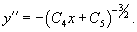 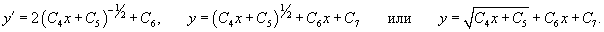 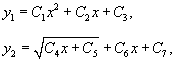 |
|
Пример 3
|
|
Найти общее решение уравнения
Решение. 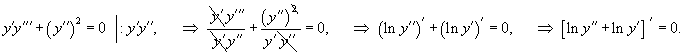 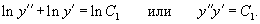 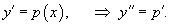 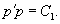 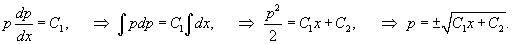 В результате получаем следующее выражение: 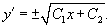 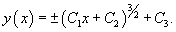 В начале решения при делении уравнения на y'' было пропущено решение 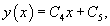 Итак, окончательный ответ содержит две ветви решений: 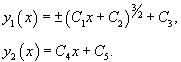 |
|
Пример 4
|
|
Найти общее решение дифференциального уравнения
Решение. 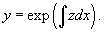 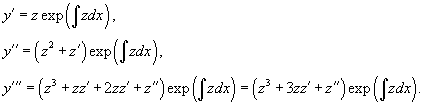 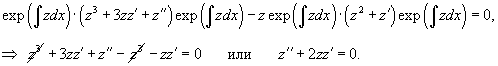 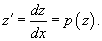 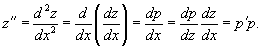 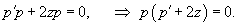 1) Первое решение определяется уравнением 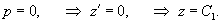 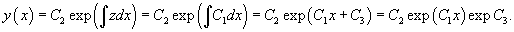 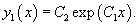 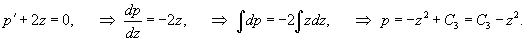 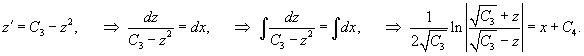 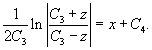 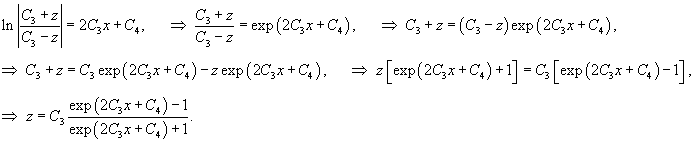 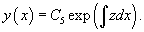 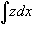 : :
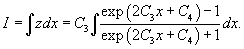 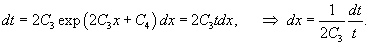 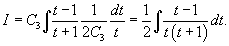 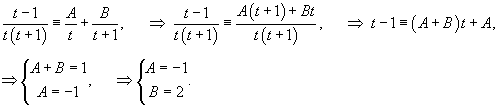 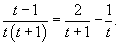 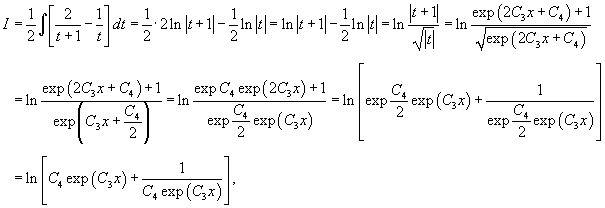 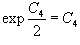 Для функции 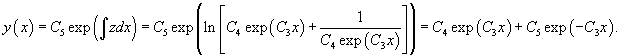 Таким образом, второе решение исходного уравнения записывается в виде 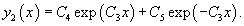 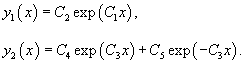 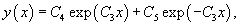 |