|
Однородные дифференциальные уравнения высшего порядка с переменными коэффициентами
|
|
Линейное однородное уравнение n-го порядка имеет вид
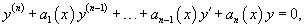 Левую часть уравнения можно записать сокращенно, используя линейный дифференциальный оператор L: 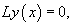 Оператор L является линейным, и, поэтому, обладает следующими свойствами:
Из свойств оператора L следует, что если функции y1, y2,..., yn являются решениями однородного дифференциального уравнения n-го порядка, то функция вида 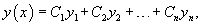 Фундаментальная система решений
Совокупность n линейно независимых частных решений y1, y2,..., yn называется фундаментальной системойлинейного однородного дифференциального уравнения n-го порядка. Функции y1, y2,..., yn являются линейно независимыми на отрезке 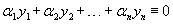 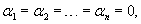 Для проверки функций на линейную независимость удобно использовать определитель Вронского иливронскиан: 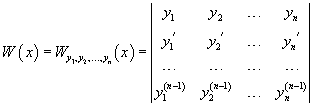 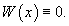 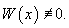 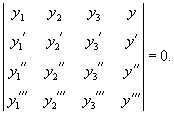 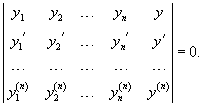 Формула Лиувилля-Остроградского
Пусть функции y1, y2,..., yn образуют фундаментальную систему решений дифференциального уравнения n-го порядка. Предположим, что точка x0 принадлежит отрезку 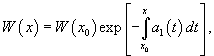 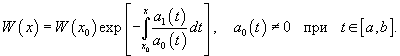 Понижение порядка однородного линейного уравнения
Порядок линейного однородного уравнения
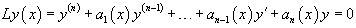 Если известно частное решение y1, то порядок дифференциального уравнения понижается (при сохранении его линейности) в результате замены 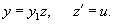 |
|
Пример 1
|
|
Показать, что функции x, sin x, cos x являются линейно независимыми.
Решение. 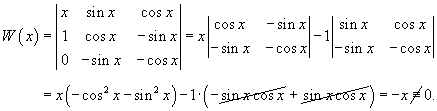 |
|
Пример 2
|
|
Показать, что функции x, x2, x3, x4 образуют линейно независимую систему.
Решение. 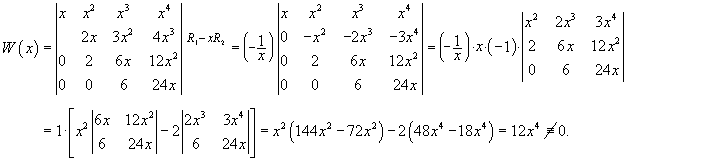 |
|
Пример 3
|
|
Составить дифференциальное уравнение, фундаментальная система которого образована функциями
Решение. 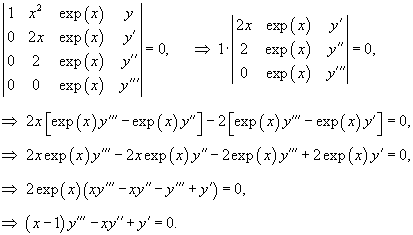 |
|
Пример 4
|
|
Найти общее решение уравнения
Решение. 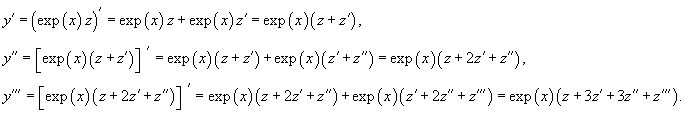 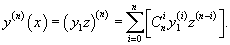 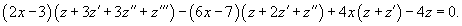 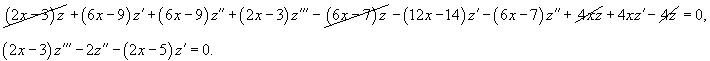 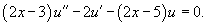 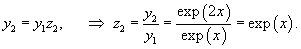 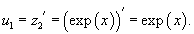 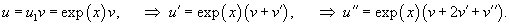 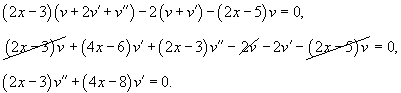 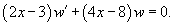 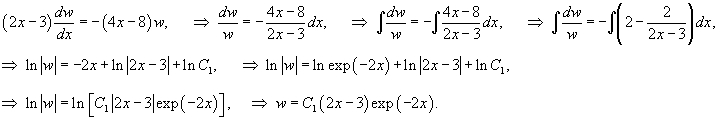 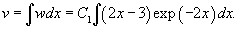 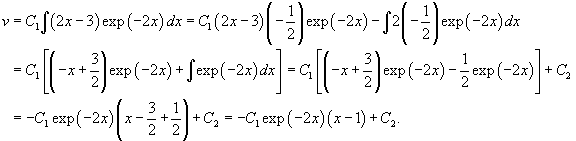 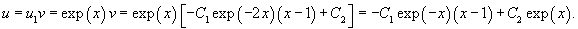 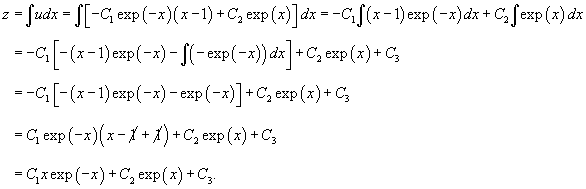 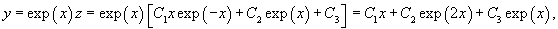 |