|
Неоднородные дифференциальные уравнения высшего порядка с постоянными коэффициентами
|
|
Данные уравнения имеют вид
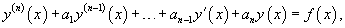 Используя линейный дифференциальный оператор 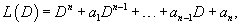 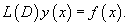 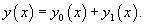 Метод вариации постоянных
Предположим, что общее решение однородного дифференциального уравнения n-го порядка известно и представляется формулой
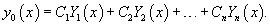 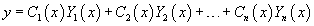 Производные n неизвестных функций 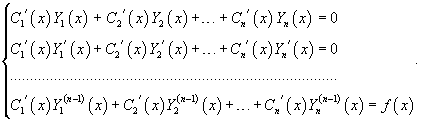 Метод неопределенных коэффициентов
Если правая часть 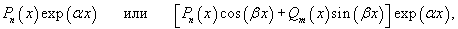 В этом случае мы ищем частное решение в форме, соответствующей структуре правой части уравнения. Так, например, для функции 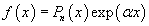 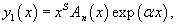 В так называемом резонансном случае, когда число α в показательной функции совпадает с корнем характеристического уравнения, в частном решении появляется дополнительный множитель xs, где s равно кратности корня. В нерезонансном случае полагают Такой же алгоритм применяется, когда правая часть уравнения задана в виде 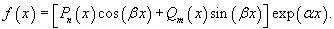 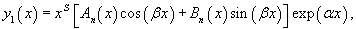 Принцип суперпозиции
Для линейных неоднородных уравнений справедлив принцип суперпозиции, который формулируется следующим образом. Пусть правая часть 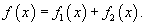 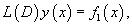 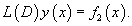 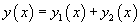 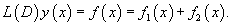 |
|
Пример 1
|
|
Найти общее решение дифференциального уравнения
Решение. 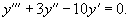 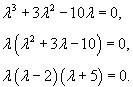 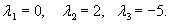 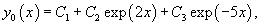 В правой части уравнения содержится лишь многочлен. Однако, если учесть, что 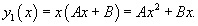 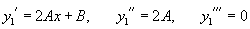 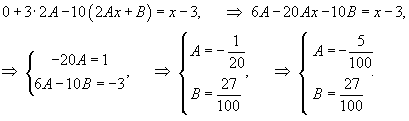 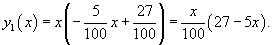 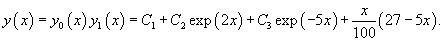 |
|
Пример 2
|
|
Решить дифференциальное уравнение
Решение. 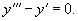 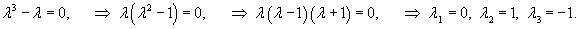 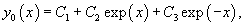 Исходя из вида правой части, будем искать частное решение в виде пробной функции 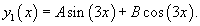 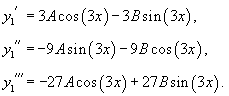 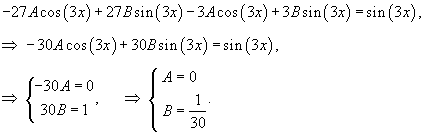 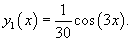 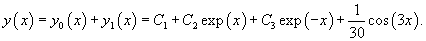 |
|
Пример 3
|
|
Решить дифференциальное уравнение
Решение. 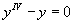 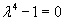 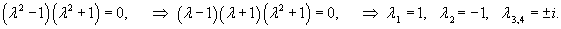 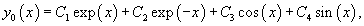 Теперь найдем частное решение неоднородного уравнения. Здесь мы имеем резонансный случай, поскольку выражение в правой части соответствует по структуре комплексному корню 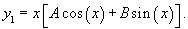 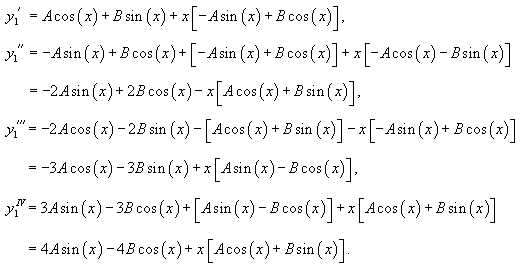 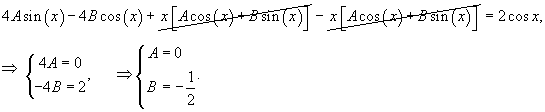 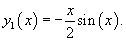 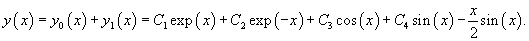 |
|
Пример 4
|
|
Решить уравнение
Решение. 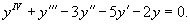 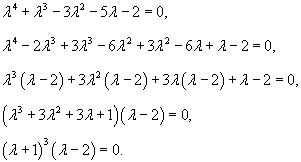 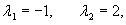 Тогда общее решение однородного уравнения записывается в виде 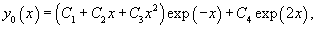 Перейдем теперь к построению частного решения неоднородного уравнения. Используя принцип суперпозиции, удобно рассмотреть два неоднородных уравнения вида 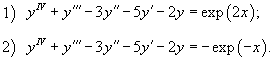 Заметим, что в обоих уравнениях возникают резонансные случаи. В первом уравнении число 2 в показателе экспоненциальной функции совпадает с корнем 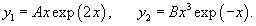 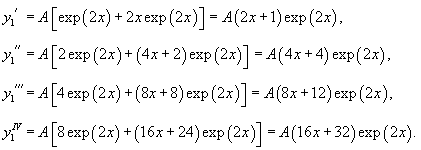 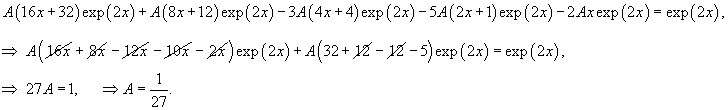 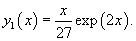 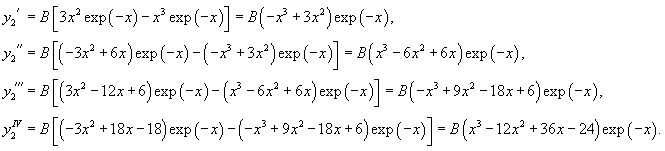 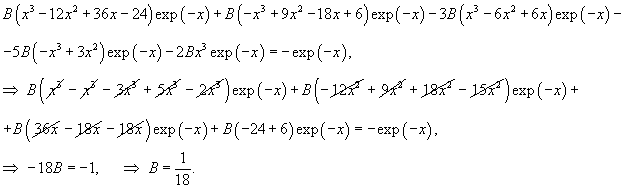 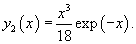 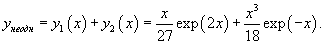 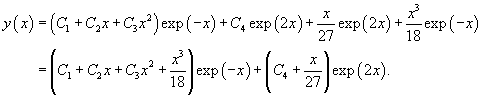 |
|
Пример 5
|
|
Найти общее решение уравнения, используя метод вариации постоянных:
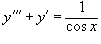 . .
Решение. 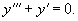 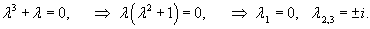 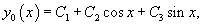 Чтобы построить общее решение неоднородного уранвения, в соответствии с методом вариации постоянных, вместо чисел C1, C2, C3 будем рассматривать функции 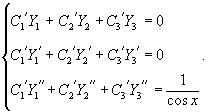 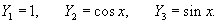 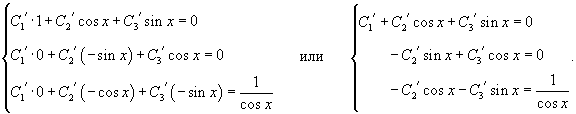 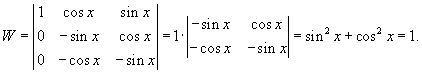 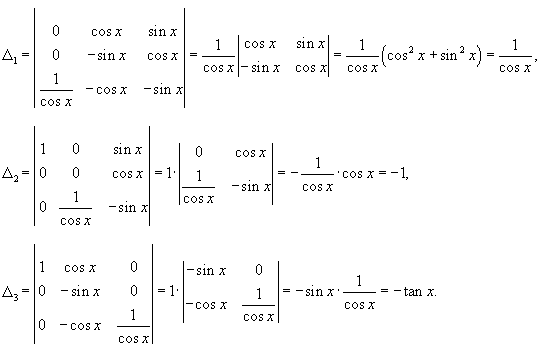 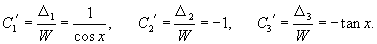 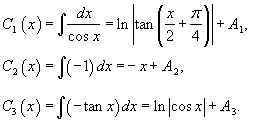 Подставляя это в общее решение, получаем ответ в следующем виде: 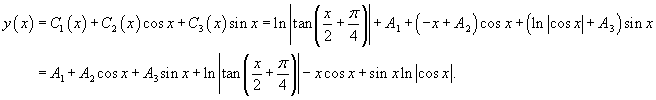 |