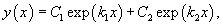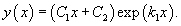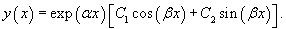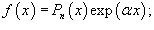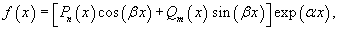|
Дифференциальные уравнения, допускающие понижение порядка
|
|
В общем случае дифференциальное уравнение второго порядка можно записать в виде
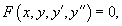 Если дифференциальное уравнение можно разрешить относительно второй производной y'', то его можно представить в следующем явном виде: 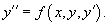 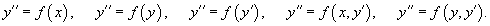 В случае произвольных дифференциальных уравнений второго порядка, их порядок можно понизить, если эти уравнения обладают определенной симметрией. Ниже мы обсудим 2 типа таких уравнений (случаи 6 и 7):
Случай 1. Уравнение вида y''= f (x)
Если дано уравнение 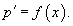 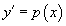 Случай 2. Уравнение вида y''= f (y)
Здесь правая часть уравнения зависит только от переменной y. Вводим новую функцию 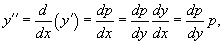 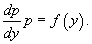 Случай 3. Уравнение вида y''= f (y' )
В данном случае для понижения порядка вводим функцию 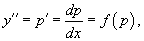 Случай 4. Уравнение вида y''= f (x,y' )
Используем подстановку 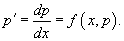 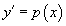 Случай 5. Уравнение вида y''= f (y,y' )
Для решения такого уравнения, также как и в случае 2, вводим новую функцию 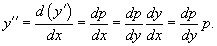 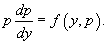 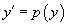 Рассмотренные 5 случаев понижения порядка не являются независимыми. Исходя из структуры уравнений, ясно, что случай 2 следует из случая 5, а случай 3 вытекает из более общего случая 4. Случай 6. Функция
Если левая часть дифференциального уравнения
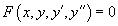 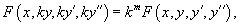 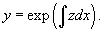 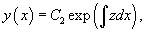 Случай 7. Функция
Если удается найти такую функцию 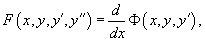 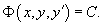 В некоторых случаях левую часть исходного уравнения можно преобразовать в точную производную, используя интегрирующий множитель. |
|
Пример 1
|
|
Решить уравнение
Решение. 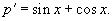 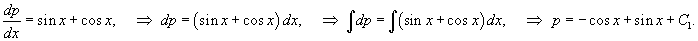 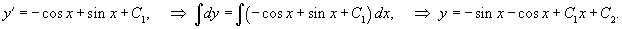 |
|
Однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
|
|
|
Рассмотрим линейное дифференциальное уравнение вида
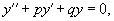 Для каждого такого дифференциального уравнения можно записать так называемое характеристическое уравнение: 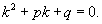
|
|
|
Пример 1
|
|
|
Решить дифференциальное уравнение
Решение. 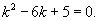 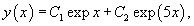 |
|
|
Пример 2
|
|
|
Найти общее решение дифференциального уравнения
Решение. 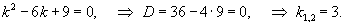 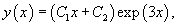 |
|
|
Пример 3
|
|
|
Решить дифференциальное уравнение
Решение. 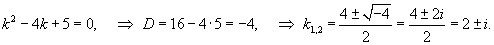 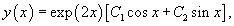 |
|
Неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
|
|
Структура общего решения
Линейное неоднородное уравнение данного типа имеет вид:
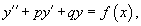 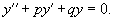 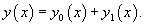 Метод вариации постоянных
Если общее решение Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид: 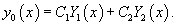 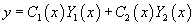 Неизвестные функции 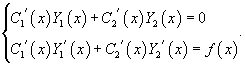 Метод неопределенных коэффициентов
Правая часть Подчеркнем, что данный метод работает лишь для ограниченного класса функций в правой части, таких как
В случае 1, если число α в экспоненциальной функции совпадает с корнем характеристического уравнения, то частное решение будет содержать дополнительный множитель xs, где s − кратность корня α в характеристическом уравнении. В случае 2, если число Неизвестные коэффициенты можно определить подстановкой найденного выражения для частного решения в исходное неоднородное дифференциальное уравнение. Принцип суперпозиции
Если правая часть неоднородного уравнения представляет собой сумму нескольких функций вида
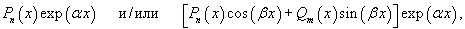 |
|
Пример 1
|
|
Решить дифференциальное уравнение Решение. 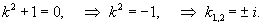 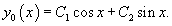 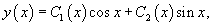 Функции 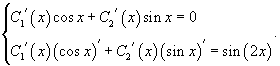 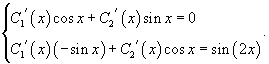 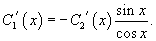 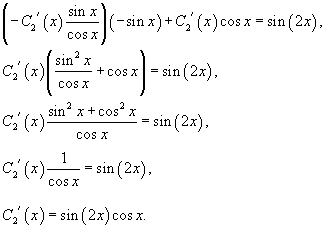 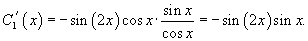 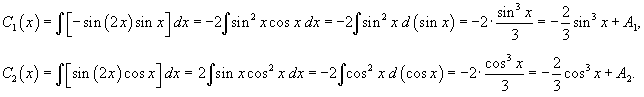 Теперь подставим найденные функции |