|
Построение общего решения системы уравнений методом неопределенных коэффициентов
|
|
Линейная однородная система n дифференциальных уравнений с постоянными коэффициентами имеет вид:
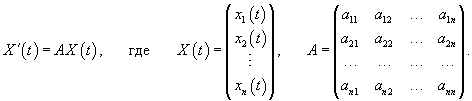 Далее мы опишем общий алгоритм решения данной системы и рассмотрим конкретные случаи, где решение строится методом неопределенных коэффициентов. Будем искать решение заданной системы уравнений в виде вектор-функций 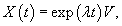 Собственные значения λi находятся из характеристического уравнения 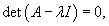 Поскольку корни λi могут быть кратными, то в общем случае для системы n-го порядка это уравнение имеет вид: 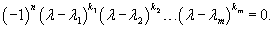 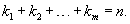 Для каждого собственного значения λi можно определить собственный вектор (или несколько собственных векторов в случае кратного λi), используя формулу 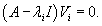 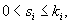 Фундаментальная система решений и, соответственно, общее решение системы существенно зависят от алгебраической и геометрической кратности чисел λi. В простейшем случае 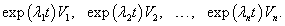 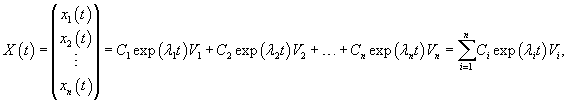 Обсудим случай комплексных корней характеристического уравнения. Если все коэффициенты в уравнениях являются действительными числами, то комплексные корни будут "рождаться" парами в виде комплексно-сопряженных чисел 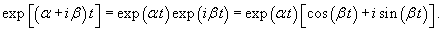 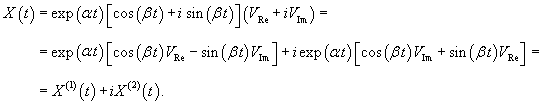 Как видно, решение для пары комплексно-сопряженных собственных значений строится таким же образом, как и для действительных собственных значений. В конце преобразований нужно лишь явно выделить действительную и мнимую части векторной функции. Теперь рассмотрим случай кратных корней λi. Для простоты будем считать их действительными. Здесь процесс решения снова разветвляется на два сценария. Если алгебраическая кратность ki и геометрическая кратность si собственного числа λi совпадают ( 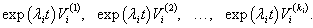 Наиболее интересным является случай кратных корней λi, когда геометрическая кратность si меньше алгебраической кратности ki. Это значит, что у нас имеется только si ( 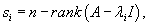 Решение, соответствующее λi, можно искать в виде произведения многочлена степени 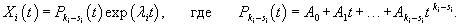 Собственно говоря, метод неопределенных коэффициентов нужен только в случае кратных корней λi, когда число линейно-независимых собственных векторов меньше алгебраической кратности корня λi. Чтобы найти векторы Описанный здесь способ построения общего решения системы однородных дифференциальных уравнений иногда называют также методом Эйлера. |
|
Пример 1
|
|
Найти общее решение линейной системы уравнений
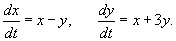 Решение.
Вычислим собственные значения λi матрицы A, составленной из коэффициентов данных уравнений:
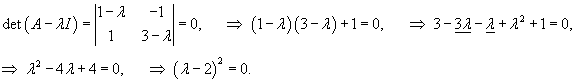 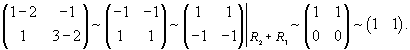 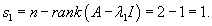 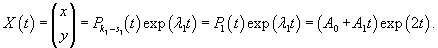 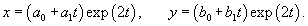 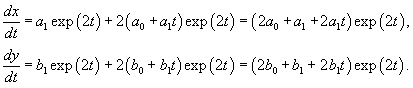 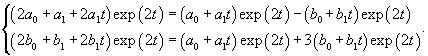 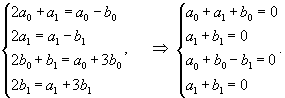 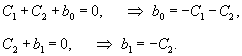 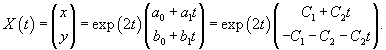 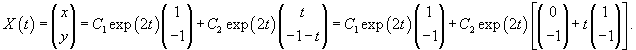 |
|
Пример 2
|
|
Найти общее решение системы уравнений
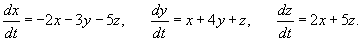 Решение.
Сначала определим собственные числа матрицы данной системы, решив соответствующее характеристическое уравнение:
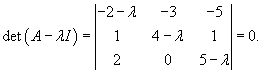 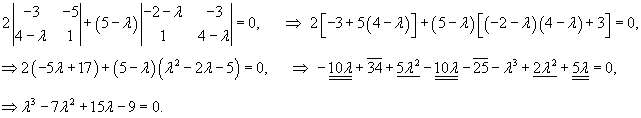 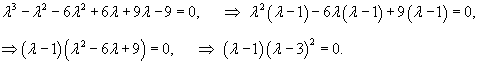 Рассмотрим первый корень 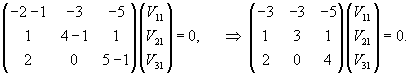 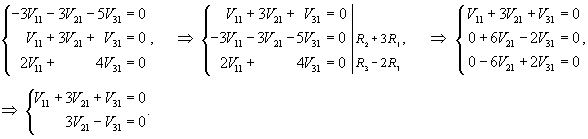 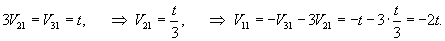 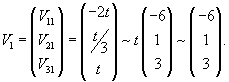 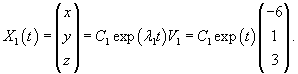 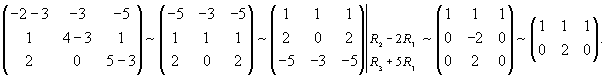 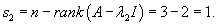 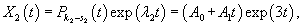 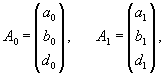 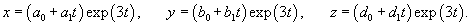 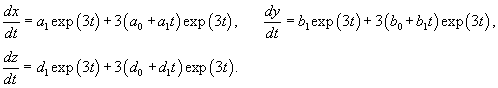 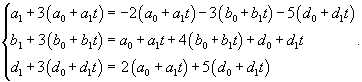 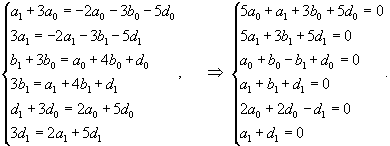 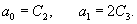 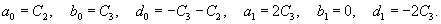 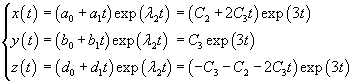 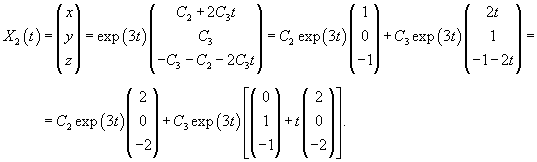 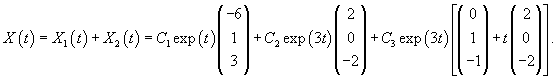 |
|
Пример 3
|
|
Найти общее решение системы дифференциальных уравнений
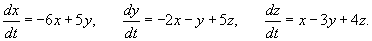 Решение.
Начнем с вычисления собственных значений матрицы данной системы. Решаем характеристическое уравнение:
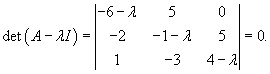 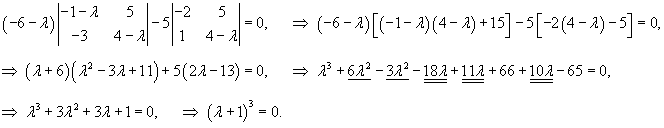 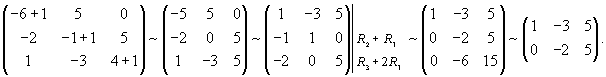 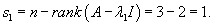 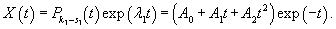 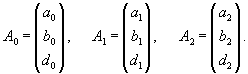 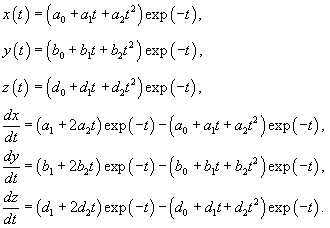 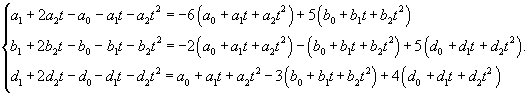 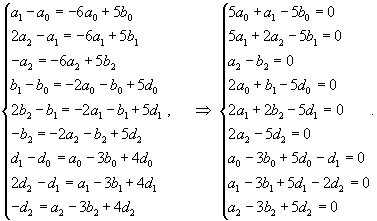 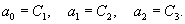 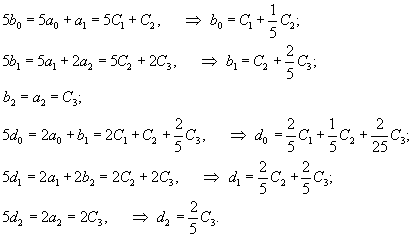 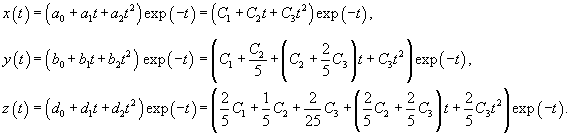 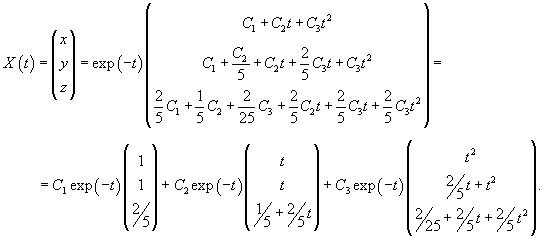 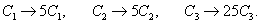 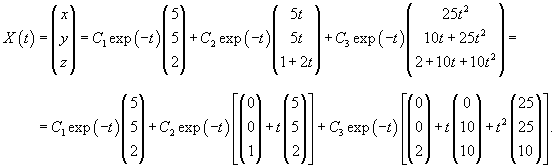 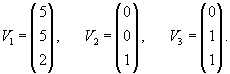 |