|
Неоднородные дифференциальные уравнения высшего порядка с переменными коэффициентами
|
|
Для полноты картины необходимо рассмотреть также неоднородные уравнения с переменными коэффициентами. Уравнения этого типа записываются в виде
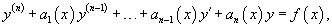 С помощью линейного дифференциального оператора L данное уравнение можно записать в компактной форме: 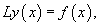 Как известно, общее решение 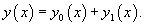 Для этой цели обычно используется метод вариации постоянных или метод Лагранжа. С помощью данного метода можно сразу получить общее решение неоднородного уравнения, если известно общее решение однородного уравнения. Метод вариации постоянных
Пусть требуется решить неоднородное уравнение n-го порядка:
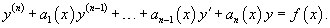 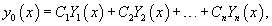 Идея данного метода состоит в том, что постоянные C1, C2,..., Cn заменяются на непрерывно дифференцируемые функции 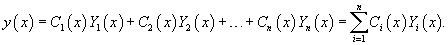 Первые производные функций 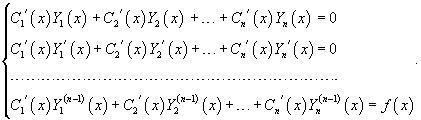 Неизвестные производные 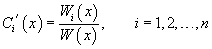 Далее выражения для 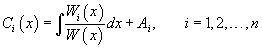 В результате общее решение неоднородного уравнения записывается в виде 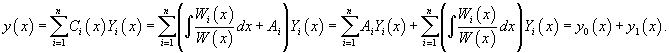 |
|
Пример
|
|
Найти общее решение дифференциального уравнения
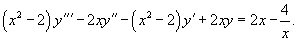 Решение.
Сначала найдем общее решение однородного уравнения
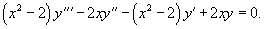 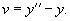 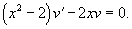 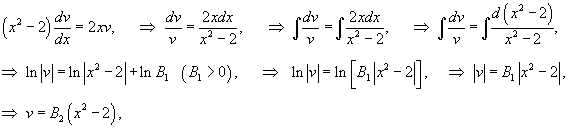 Найдем теперь функцию 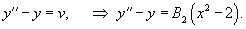 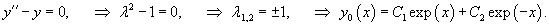 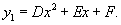 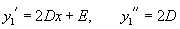 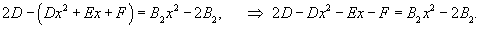 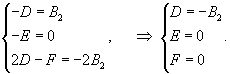 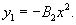 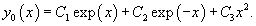 Теперь найдем решение неоднородного уравнения, используя метод вариации постоянных. Общее решение уравнения представляется в виде 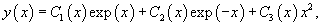 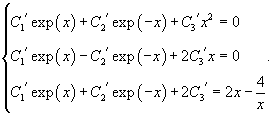 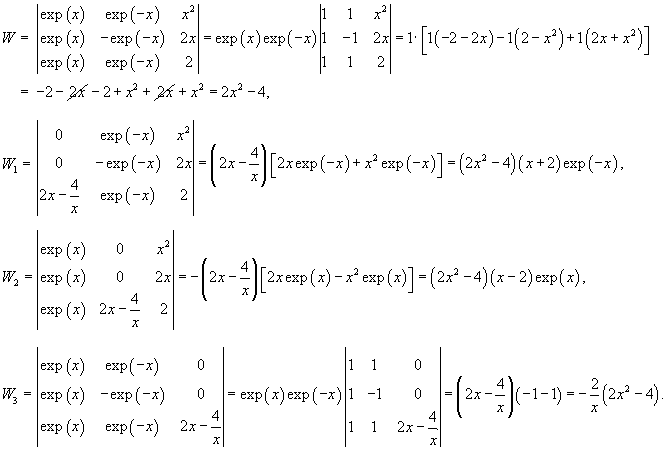 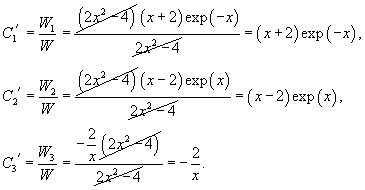 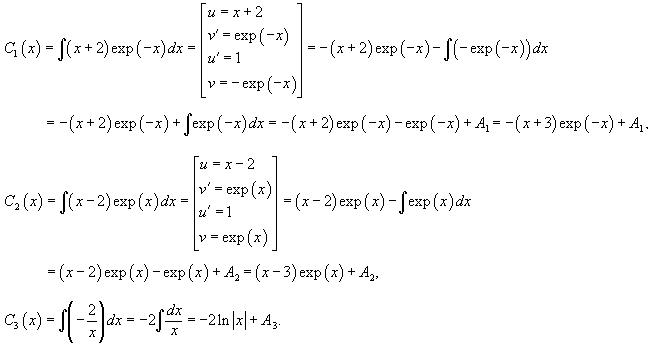 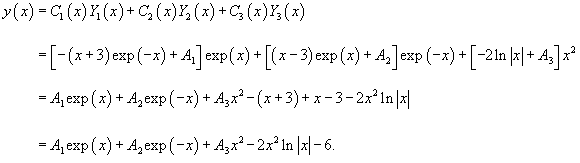 |