|
Однородные дифференциальные уравнения второго порядка с переменными коэффициентами
|
|
Линейное однородное уравнение второго порядка с переменными коэффициентами записывается в виде
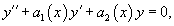 Линейная независимость функций. Определитель Вронского
Функции 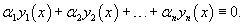 Для случая двух функций критерий линейной независимости можно записать в более простом виде: Функции 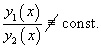 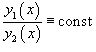 , эти функции будут линейно зависимыми. , эти функции будут линейно зависимыми. Пусть n функций 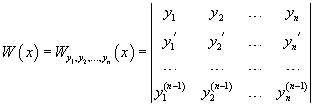 Теорема. Если система функций Отсюда следует, что если определитель отличен от нуля хотя бы в одной точке отрезка Фундаментальная система решений
Совокупность двух линейно независимых частных решений линейного однородного дифференциального уравнения второго порядка образует его фундаментальную систему решений. Если 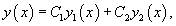 Заметим, что по заданной фундаментальной системе решений 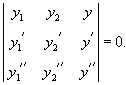 Формула Лиувилля-Остроградского
Итак, как указано выше, общее решение однородного дифференциального уравнения второго порядка является линейной комбинацией двух линейно независимых частных решений Очевидно, что частные решения зависят от коэффициентов дифференциального уравнения. Формула Лиувилля-Остроградского устанавливает связь между вронскианом Пусть 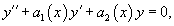 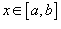 справедлива формула Лиувилля-Остроградского: справедлива формула Лиувилля-Остроградского:
 Практические методы решения однородных уравнений 2-го порядка с переменными коэффициентами
К сожалению, общего метода отыскания частного решения не существует. Обычно это можно сделать путем подбора. Если известно частное решение Другой способ понижения порядка основан на использовании формулы Лиувилля-Остроградского. Здесь также одно частное решение |
|
Пример 1
|
|
Исследовать, являются ли функции
Решение. 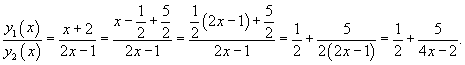 |
|
Неоднородные дифференциальные уравнения второго порядка с переменными коэффициентами
|
|
Определение и общая схема решения
Линейное неоднородное уравнение второго порядка с переменными коэффициентами имеет вид
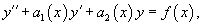 Соответствующее однородное уравнение записывается в виде 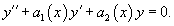 
Метод вариации постоянных
Метод вариации постоянных (или метод Лагранжа) используется для построения общего решения неоднородного уравнения, когда известно общее решение ассоциированного с ним однородного уравнения. Пусть общее решение однородного уравнения 2-го порядка выражается через фундаментальную систему решений 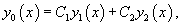 Производные неизвестных функций 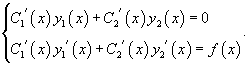 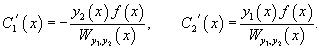 Далее, зная производные 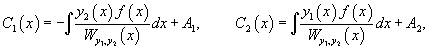 Тогда общее решение исходного неоднородного уравнения будет выражаться формулой 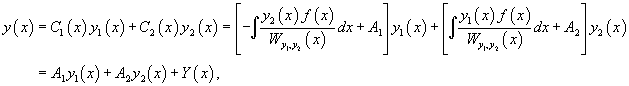 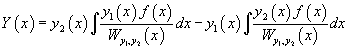 |
|
Пример 1
|
|
Найти общее решение дифференциального уравнения
Решение. 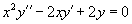 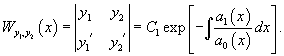 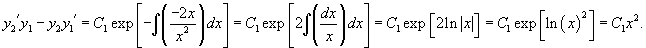 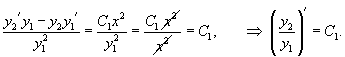 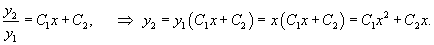 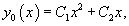 Теперь воспользуемся методом вариации постоянных и построим общее решение неоднородного уравнения. Будем рассматривать параметры C1 и C2 как функции от переменной x. Производные этих функций определяются из системы уравнений 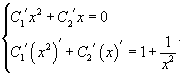 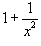 во втором уравнении записана после преобразования исходного дифференциального уравнения в стандартную форму: во втором уравнении записана после преобразования исходного дифференциального уравнения в стандартную форму:
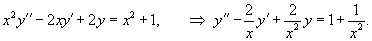 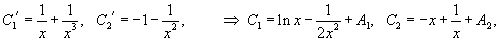 В результате получаем общее решение неоднородного уравнения в виде 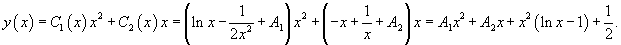 |