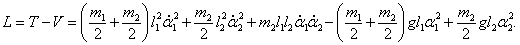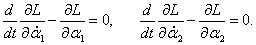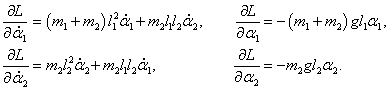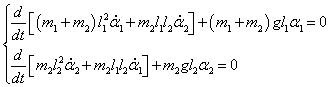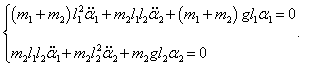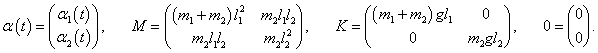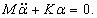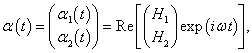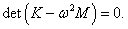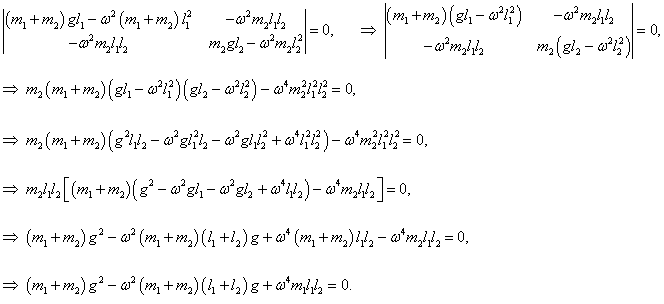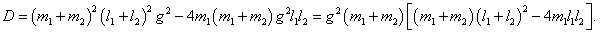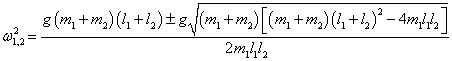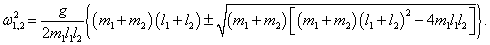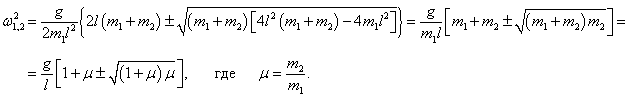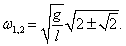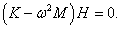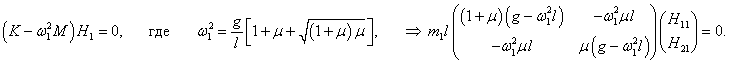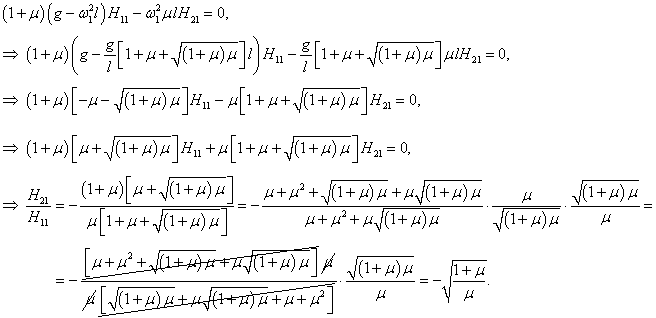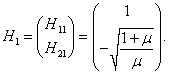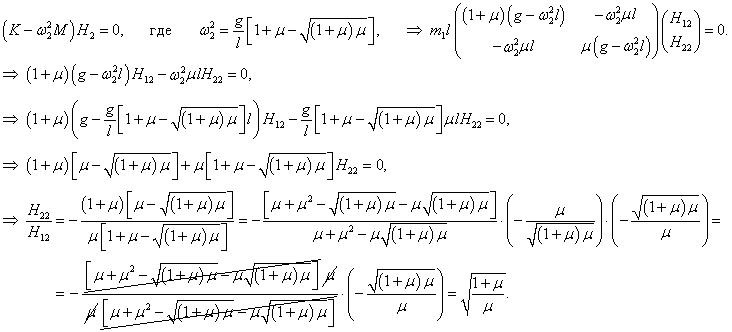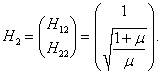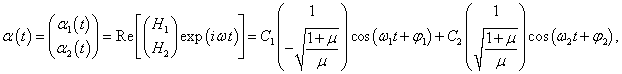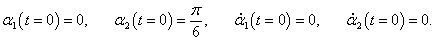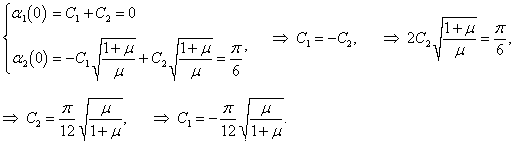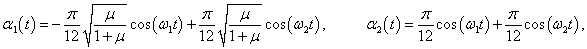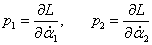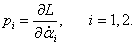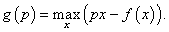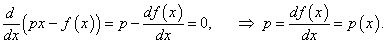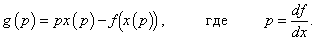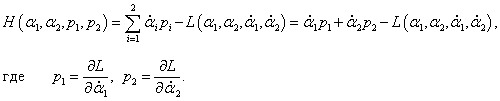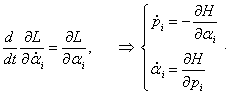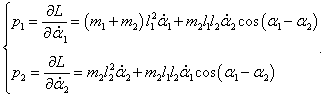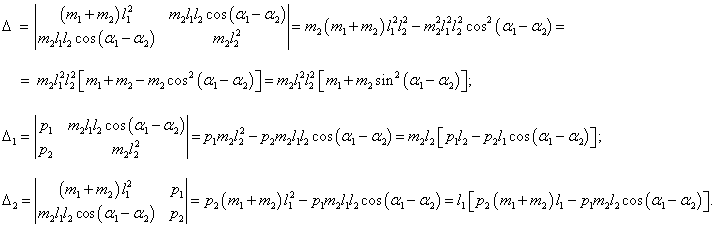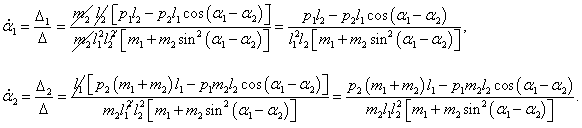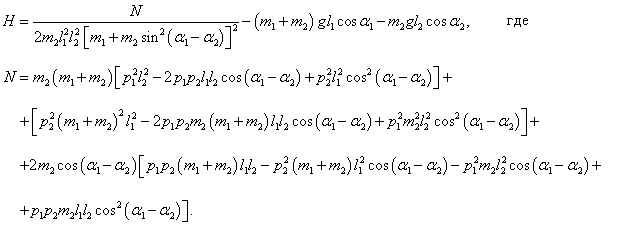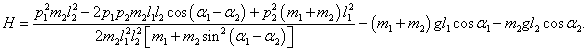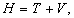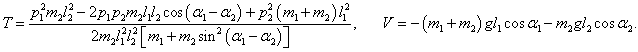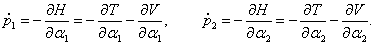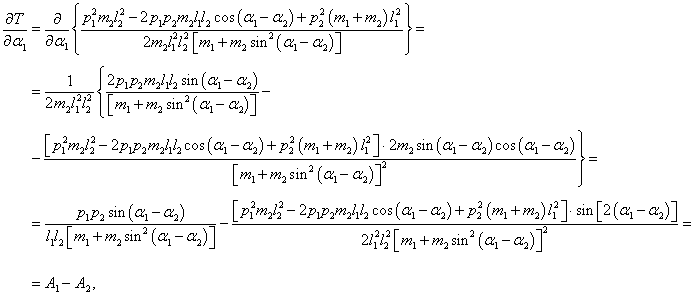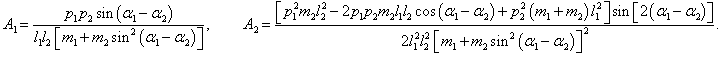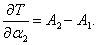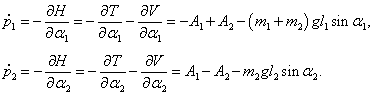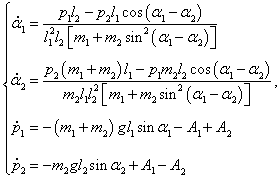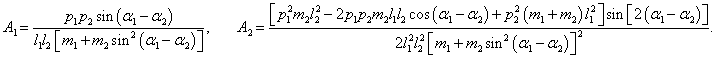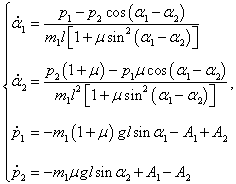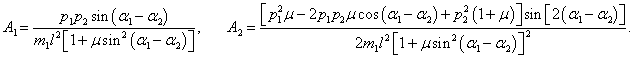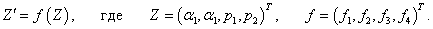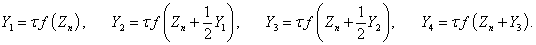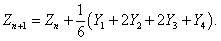Двойной маятник - это, несомненно, настоящее чудо природы. Поразителен скачок сложности, который наблюдается при переходе от простого одиночного маятника к двойному. Колебания простого маятника имеют регулярный характер. При малых отклонениях от равновесия такие колебания являются гармоническими и описываются функцией синус или косинус. В случае
нелинейных колебаний период зависит от амплитуды, но регулярность движения сохраняется. Другими словами, в случае простого маятника приближение малых колебаний вполне отражает существенные свойства системы.
Двойной маятник "ведет себя" совершенно иначе. Уже в режиме малых колебаний у двойного маятника возникает такое новое явление как
эффект биений. А при увеличении энергии характер колебаний маятников меняется принципиально − колебания становятся
хаотическими. Несмотря на то, что двойной маятник можно описать системой нескольких обыкновенных дифференциальных уравнений, то есть вполне детерминированной моделью, появление хаоса выглядит очень необычно. Данная ситуация напоминает
систему Лоренца, где детерминированная модель из трех уравнений также демонстрирует хаотическое поведение. Попробуйте поэкспериментировать с приведенным ниже приложением и понаблюдайте за движением двойного маятника при различных отношениях масс тел и начальных углах.
Далее мы займемся построением математической модели двойного маятника в виде системы нелинейных дифференциальных уравнений. Начнем с вывода
уравнений Лагранжа.
Уравнения Лагранжа
В лагранжевой механике для описания системы используются
обобщенные координаты и
обобщенные скорости. В нашем случае в качестве таких переменных можно взять углы отклонения маятников
α1,
α2 и угловые скорости
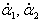
. Используя указанные переменные, построим
лагранжиан двойного маятника и запишем дифференциальные уравнения Лагранжа.
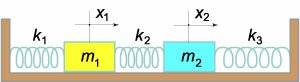
Упрощенная модель двойного маятника показана на рисунке 1. Будем считать стержни невесомыми. Их длины равны
l1 и
l2. Массы точечных тел (они представлены шарами конечного радиуса) составляют
m1 и
m2. В точках подвеса трение отсутствует.
Введем систему координат O
xy, начало которой совпадает с точкой подвеса. Координаты маятников определяются следующими соотношениями:
Кинетическая и потенциальная энергия маятников (соответственно
T и
V) выражаются формулами
Тогда лагранжиан записывается в виде
Учтем, что
Следовательно,
В результате лагранжиан системы принимает такой вид:
Теперь мы можем составить
уравнения Лагранжа (иногда их называют
уравнениями Эйлера-Лагранжа):
Входящие в уравнения частные производные выражаются следующими формулами:
Следовательно, первое уравнение Лагранжа записывается как
Сокращая на
l1 ≠ 0, получаем:
Аналогично выведем второе дифференциальное уравнение:
После сокращения на
m2l1 ≠ 0 уравнение принимает такой вид:
Таким образом, нелинейная система двух дифференциальных уравнений Лагранжа записывается как
Малые колебания двойного маятника
Если считать углы
α1(t),
α2(t) малыми, то колебания маятников вблизи нулевого положения равновесия можно описать линейной системой уравнений. Чтобы получить такую систему, вернемся назад к исходному лагранжиану системы:
Запишем этот лагранжиан в более простом виде, раскладывая его в ряд Маклорена и сохраняя линейные и квадратичные члены. Тригонометрические функции можно заменить следующими приближенными выражениями:
Здесь мы учли, что слагаемое с
cos(α1 − α2) содержит произведение малых величин
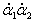
и имеет второй порядок малости. Поэтому в разложении косинуса можно ограничиться линейным членом.
Подставляя это в исходный лагранжиан и учитывая, что потенциальная энергия определяется с точностью до константы, получаем квадратичный лагранжиан двойного маятника в виде:
Выведем дифференциальные уравнения Лагранжа для данного лагранжиана. Они записываются в таком виде:
Найдем частные производные:
Получаем систему двух дифференциальных уравнений Лагранжа:
или
Данную систему уравнений можно записать в компактной матричной форме. Введем матрицы
Тогда система дифференциальных уравнений представляется в виде
В случае одного тела такое уравнение описывает свободные незатухающие колебания с определенной частотой. В случае двойного маятника решение (как вы увидим ниже) будет содержать колебания с двумя характерными частотами, которые называются
нормальными модами. Нормальные моды представляют собой действительную часть комплекснозначной векторной функции
где
H1,
H2 − собственные векторы,
ω − действительная частота. Значения нормальных частот
ω1, 2 определяются из решения характеристического уравнения
Выведем общие формулы для циклических частот
ω1, 2 в случае произвольных масс
m1,
m2 и длин
l1,
l2:
Мы получили биквадратное уравнение для частот
ω. Вычислим дискриминант:
Таким образом, квадраты нормальных частот
ω1, 2 равны
или
Данное выражение является несколько громоздким. Поэтому далее рассмотрим случай, когда длины стержней обоих маятников равны:
l1 = l2 = l. Тогда нормальные частоты будут определяться более компактной формулой
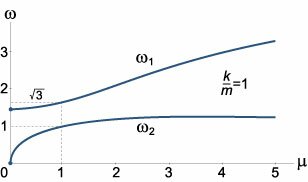
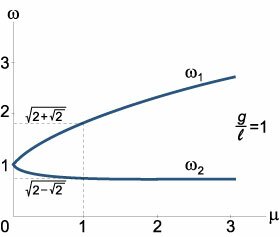
Как видно, собственные частоты
ω1, 2 зависят лишь от отношения масс
μ = m2/m1. Зависимости частот
ω1,
ω2 от параметра
μ (при условии
g/l = 1) показаны выше на рисунке 2. В частности, при равных массах
m1 = m2 = m, т.е. при
μ = 1, собственные частоты равны
Теперь, после того как собственные частоты
ω1, 2 известны, для описания нормальных мод нужно определить еще
собственные векторы H1, 2. Они находятся из решения векторно-матричного уравнения
Пусть собственный вектор
H1 = (H11, H21) T (верхний индекс
T означает операцию транспонирования) соответствует нормальной частоте
ω1. Тогда получаем следующее уравнение для определения
H1:
Координаты собственного вектора
H1 удовлетворяют уравнению
Таким образом, собственный вектор
H1 равен
Аналогичным образом найдем координаты второго собственного вектора
H2 = (H12, H22) T :
Следовательно, собственный вектор
H2 имеет такие координаты:
Общее решение матричного уравнения записывается в виде
где постоянные
C1,
C2,
φ1,
φ2 зависят от начальных положений и скоростей маятников.
Рассмотрим характер малых колебаний для некоторого конкретного набора начальных данных. Пусть, например, координаты и скорости маятников в начальный момент имеют такие значения:
В этом случае начальные фазы равны нулю:
φ1 = φ2 = 0. Определим постоянные
C1 и
C2:
Тогда закон колебаний маятников выражается формулами
где циклические частоты
ω1, 2 определяются соотношением
Здесь углы
α1(t),
α2(t) выражаются в радианах, а время
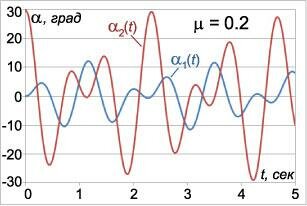
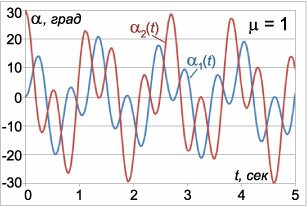
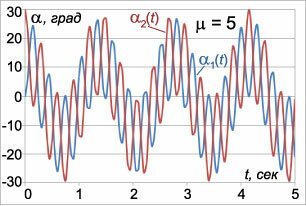
t в секундах. На рисунках 3-5 приведены графики малых колебаний маятников для трех значений
μ:
μ1 = 0.2,
μ2 = 1,
μ3 = 5, при условии
l = l1 = l2 = 0.25 м,
g = 9.8 м/c2. Углы отклонения маятников для удобства приведены в градусах. Из графиков видно, что в системе происходят
биения, при которых энергия циклически переходит от одного маятника к другому. Когда один маятник почти останавливается, другой раскачивается с максимальной амплитудой. Через некоторое время маятники "меняются ролями" и так далее. Колебания с большей частотой
ω1 модулируются более низкочастотными колебаниями с частотой
ω2. Это особенно хорошо заметно на рисунке 5 при большом значении
μ (
μ3 = 5), когда разница между частотами
ω1 и
ω2 велика.
Итак, малые колебания двойного маятника имеют периодический характер и описываются суммой двух гармоник с частотами
ω1,
ω2, зависящими от параметров системы. Характерным свойством малых колебаний двойного маятника является
эффект биений.
Преобразование Лежандра и уравнения Гамильтона
Вернемся теперь снова к исходной нелинейной системе уравнений и исследуем характер колебаний с произвольной амплитудой. Такая система уравнений не решается аналитически. Поэтому мы будем рассматривать
численную модель двойного маятника.
Приведенные выше уравнения Лагранжа являются дифференциальными уравнениями второго порядка. Их удобнее преобразовать в форму
канонических уравнений Гамильтона. В результате вместо 2 уравнений второго порядка мы получим систему 4 дифференциальных уравнений первого порядка.
В гамильтоновой механике состояние системы определяется
обобщенными координатами и
обобщенными импульсами. В нашем случае в качестве обобщенных координат мы снова, как и в уравнениях Лагранжа, будем использовать углы
α1,
α2. Вместо обобщенных скоростей
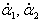
(в лагранжиане) введем теперь обобщенные импульсы
p1,
p2, связанные со скоростями формулами
или в краткой записи:
Переход от лагранжевой к гамильтоновой форме уравнений производится с помощью
преобразования Лежандра, которое определяется следующим образом.
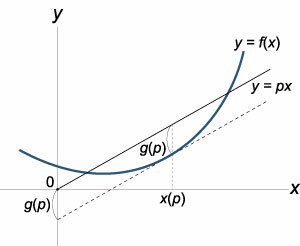
Предположим, что
f(
x) − гладкая выпуклая вниз функция (рисунок 6). Рассмотрим прямую
y = px, проходящую через начало координат. Расстояние между прямой
y = px и функцией
y = f(x) вдоль оси O
y зависит от координаты
x. При определенном значении
x это расстояние будет максимальным. Ясно, что оно зависит от наклона прямой, т.е. от параметра
p. Таким образом мы вводим новую функцию
g(
p):
Такое преобразование функции
f(
x) в сопряженную функцию
g(
p) называется
преобразованием Лежандра. Заметим, что функция
g(
p) достигает максимального значения по переменной
x когда
p = df/dx. Действительно,
Зная зависимость
p(
x), можно найти обратную функцию
x(
p). Тогда преобразование Лежандра будет выражаться соотношением
Преобразование Лежандра легко обобщается на случай функций нескольких переменных. В модели двойного маятника переход от функции Лагранжа к функции Гамильтона описывается преобразованием Лежандра в форме:
В этом выражении
L является лагранжианом, а функция
H представляет собой
гамильтониан системы, который зависит от обобщенных координат
α1,
α2 и обобщенных импульсов
p1,
p2.
В результате такого преобразования каждое уравнение Лагранжа переходит в систему двух канонических уравнений Гамильтона, имеющих вид:
Определим теперь конкретный вид уравнений Гамильтона для двойного маятника. Обобщенные импульсы
p1,
p2 выражаются через частные производные лагранжиана в виде
Решим эту систему уравнений и выразим угловые скорости через обобщенные координаты и импульсы. Воспользуемся
формулами Крамера и вычислим соответствующие определители:
Отсюда получаем следующие выражения для угловых скоростей:
Эти формулы представляют собой первые 2 (из 4) дифференциальных уравнений Гамильтона. С учетом данных выражений гамильтониан можно записать в следующем виде:
Последнюю формулу можно представить как
Числитель
N в этом выражении является весьма громоздким. Упростим его:
Следовательно, функция Гамильтона принимает такой вид:
Здесь первое слагаемое представляет собой
обобщенную кинетическую энергию T, а два других слагаемых −
потенциальную энергию V, т.е. гамильтониан
H определяется как
где
Теперь мы можем составить еще два дифференциальных уравнения Гамильтона для обобщенных импульсов:
Вычислим отдельно частные производные обобщенной кинетической энергии:
где символами
A1 и
A2 обозначены выражения
Производная кинетической энергии
T по переменной
α2 будет иметь такой же вид, только с противоположным знаком:
Отсюда получаем уравнения Гамильтона в виде:
Итак, в результате громоздких преобразований мы получили то, к чему так долго стремились − систему 4 канонических уравнений Гамильтона, описывающих движение двойного маятника. Запишем их вместе в окончательном виде:
где
Теперь можно приступить к численному анализу уравнений.
Численное моделирование хаотических колебаний
Наиболее распространенным методом численного решения дифференциальных уравнений является
метод Рунге-Кутты 4-го или 5-го порядка точности. Различные вариации этого метода используются в большинстве математических пакетов (MatLab, Maple, Mathematica, Mathcad), как правило, с автоматическим контролем точности и адаптивным временным шагом.
Для моделирования движения двойного маятника мы также воспользуемся классическим методом Рунге-Кутты 4-го порядка точности. Предварительно несколько упростим дифференциальные уравнения, полагая, что длины маятников одинаковы:
l1 = l2 = l. Введем также параметр
μ, равный отношению массы второго маятника к массе первого:
μ = m2/m1. Тогда система уравнений принимает следующий вид:
где
Данную систему можно переписать в векторной форме:
Вектор
Z составлен из 4-х канонических переменных данной системы, а компоненты вектора
f соответствуют правым частям дифференциальных уравнений.
Метод Рунге-Кутты предполагает на каждом шаге последовательное вычисление четырех промежуточных векторов:
Значение вектора
Zn+1 в следующем временном узле вычисляется по формуле
Суммарная ошибка данного алгоритма на конечном интервале имеет порядок
O(τ4 ), т.е. точность вычислений возрастает в 16 раз при уменьшении временного шага
τ в два раза.
Описанная модель реализована в анимации, приведенной в начале web-страницы. Для упрощения мы положили начальные углы отклонения маятников равными:
α1 = α2 = α. Данное приложение наглядно демонстрирует хаотическую динамику двойного маятника при различных значениях параметров
μ и
α. Интересно,
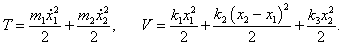
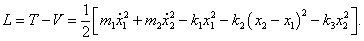
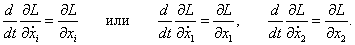
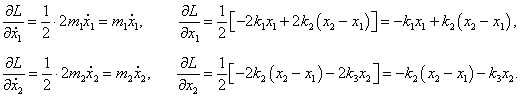
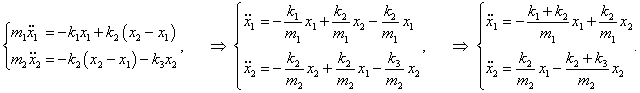
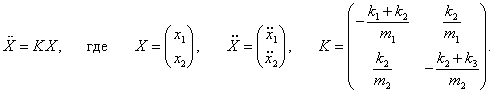
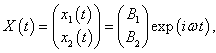
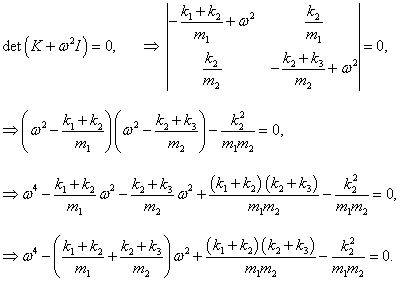
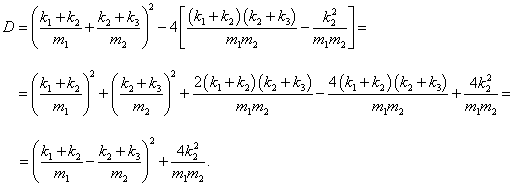
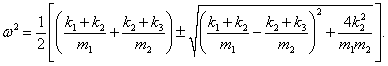
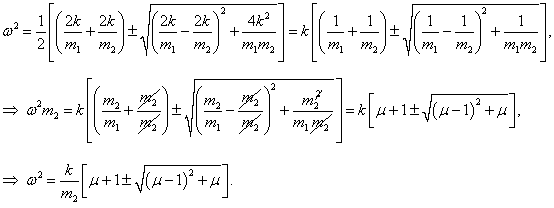
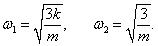
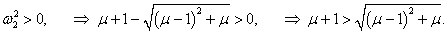
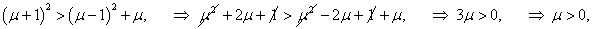
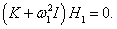
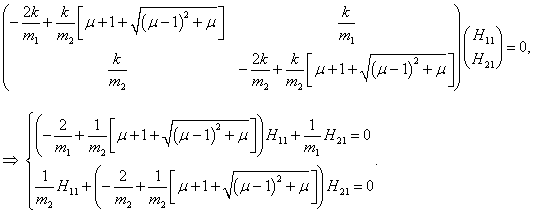
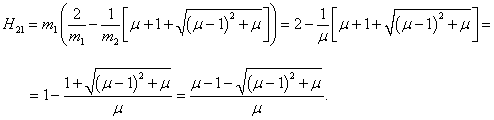
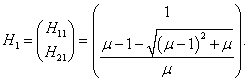
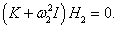
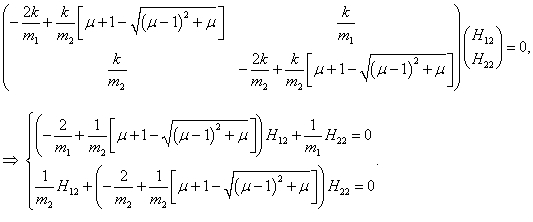
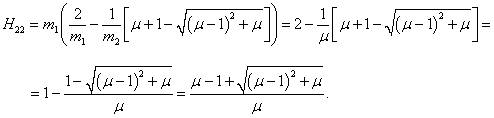
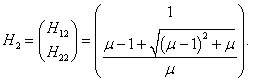
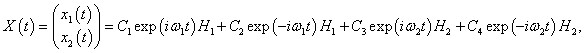

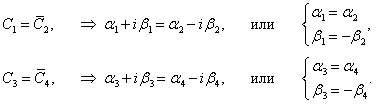
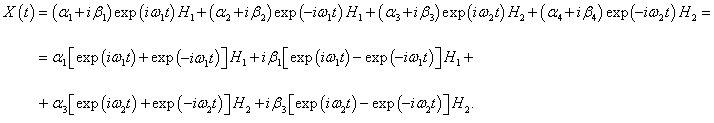
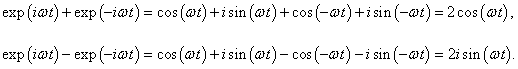
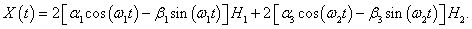
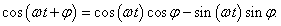
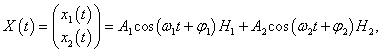
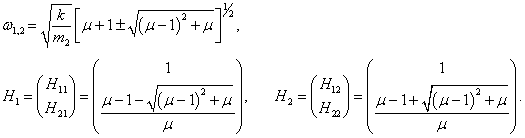
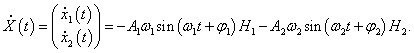
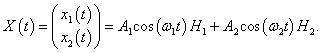
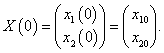
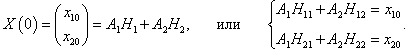
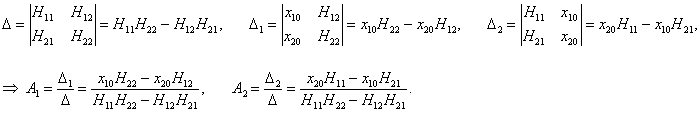
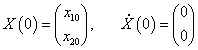
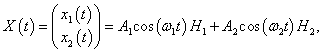
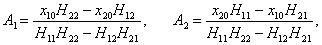
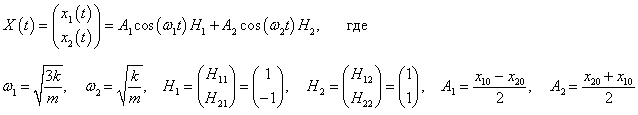
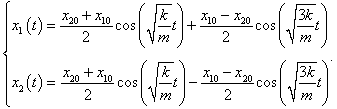
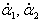 . Используя указанные переменные, построим
. Используя указанные переменные, построим 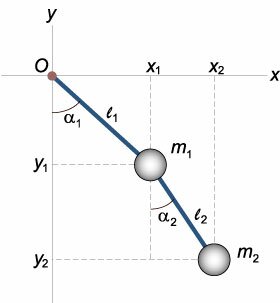
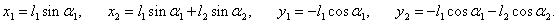
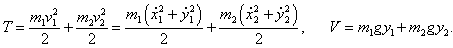
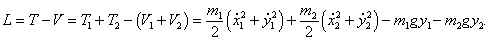
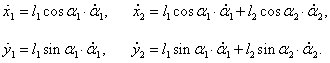

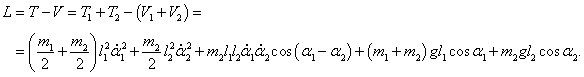
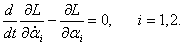
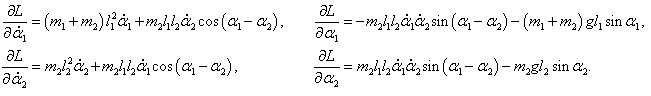
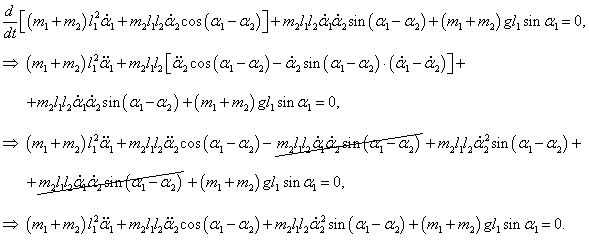
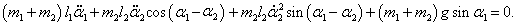
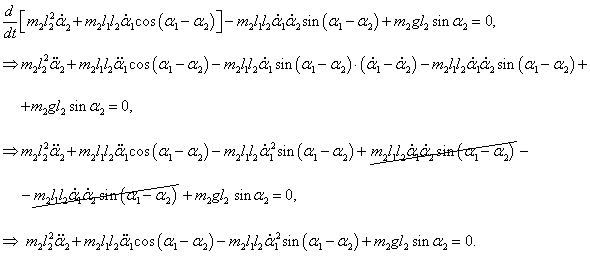
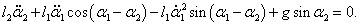
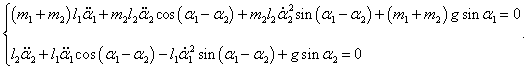
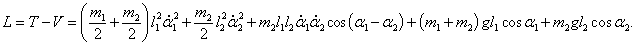
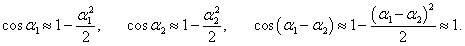
 и имеет второй порядок малости. Поэтому в разложении косинуса можно ограничиться линейным членом.
и имеет второй порядок малости. Поэтому в разложении косинуса можно ограничиться линейным членом.