|
Однородные дифференциальные уравнения высшего порядка с постоянными коэффициентами
|
|
Линейное однородное дифференциальное уравнение n-го порядка с постоянными коэффициентамизаписывается в виде
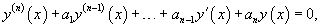 Используя линейный дифференциальный оператор 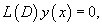 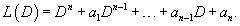 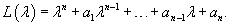 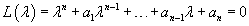 Согласно основной теореме алгебры, многочлен степени n имеет ровно n корней с учетом их кратности. При этом корни уравнения могут быть как действительными, так и комплексными (даже если все коэффициентыa1, a2,..., an действительные). Рассмотрим более детально различные случаи корней характеристического уравнения и соответствующие формулы общего решения дифференциального уравнения. Случай 1. Все корни характеристического уравнения действительные и различные
Предположим, что характеристическое уравнение 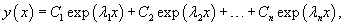 Случай 2. Корни характеристического уравнения действительные и кратные
Пусть характеристическое уравнение 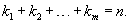 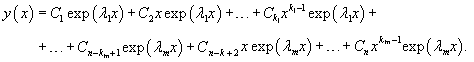 Случай 3. Корни характеристического уравнения комплексные и различные
Если коэффициенты дифференциального уравнения являются действительными числами, то комплексные корни характеристического уравнения будут представляться в виде пар комплексно-сопряженных чисел:
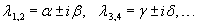 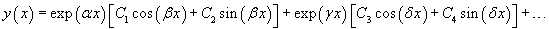 Случай 4. Корни характеристического уравнения комплексные и кратные
Здесь каждой паре комплексно-сопряженных корней 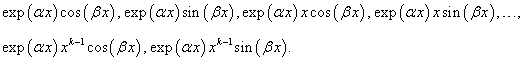 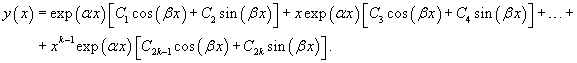 |
|
Пример 1
|
|
Решить дифференциальное уравнение
Решение. 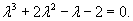 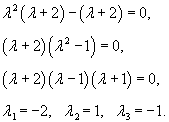 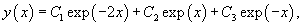 |
|
Пример 2
|
|
Решить уравнение
Решение. 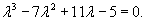 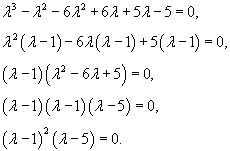 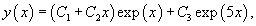 |
|
Пример 3
|
|
Решить уравнение
Решение. 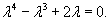 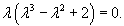 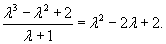 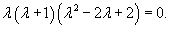 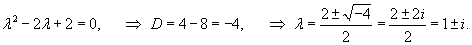 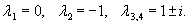 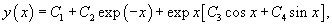 |
|
Пример 4
|
|
Решить уравнение
Решение. 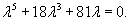 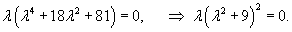 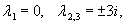 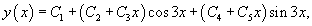 |
|
Пример 5
|
|
Решить уравнение
Решение. 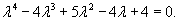 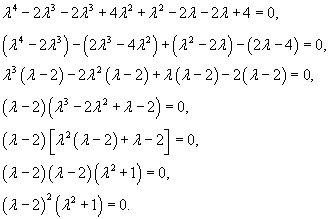 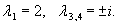 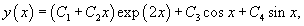 |